Hello. My name is Joe Boaler, and I’m a professor at Stanford University in California and co-founder of Youcubed.org, which is a site to bring free maths resources to help improve the teaching of mathematics. I started my career as a teacher in London and then worked at King’s College London before moving to California.
In the classroom that we just saw, there were so many things that were really important that I want to highlight. The students were learning mathematics through problem solving.
They were developing number sense, but they were using and applying their own ideas. With student agency at the fore, the mathematics was multidimensional, and students were learning about numbers and number groups through words, through their own talk, through their physical manipulatives they were holding in their hand. The teacher had really deemphasized speed. She gives students time to think deeply. She highlights, as you saw, struggle and the importance of struggle.
And the students are working together to see and understand mathematical connections. The task, the penny task, it actually comes, the task we made it’s on our website, but comes from the Chinese remainder theorem. Ask students to look for patterns as they think about groups, and many mathematical standards are taught inside the task. And I’ve put a list of them up there.
So one of the things I want to highlight today, one of the areas that I’m working on and try to spread as widely as possible, is the fact that we know that struggle, times of struggle, is really the very best time for our brains. It’s when our brains are on fire with connections and growth, and that we should want students to be at the edge of their understanding. That’s a really important place to be. This is coming from neuroscience and what we know about the brain. But I am aware that the giants of psychology have been sharing the importance of this time for many years.
Vigotsky talked about the zone of proximal development, the space between what a learner can do with and without assistance. And of course, that is also a time when students are really struggling at the edge of their understanding. And Piaget, of course, taught us about the importance of being in disequilibrium.
So there has been a lot of work on mindset and amazing evidence of the importance of mindset. But recently, I’m seeing some pushback against mindset, where people are saying it doesn’t work or the effects are very minimal. And that happens when people come into education spaces, tell students they can learn anything, and then leave, and the teaching stays the same. The very latest evidence tells us that we know that mindset is really impactful. And really works when a mindset culture is developed inside classrooms, when students know about the importance of struggle, and when they know that their brains are connecting and growing all the time, but when mathematics is also taught as a growth subject and assessed with different opportunities for students to grow and learn.
And on our website, Youcubed, we have a new section that shares the very latest evidence on the importance of developing a mindset culture. I have a resource that’s been really helpful to a lot of people. It’s a free online class for students. 6-15 minutes. Sessions that share about mindset, also some different strategies for approaching maths. And we’ve studied this with a randomized controlled trial where middle school teachers, who had two classes of students, gave this online class just to one of these classes. And what they found, even though that it was the same teacher teaching the different classes, those who had had this short online class achieved at significantly higher levels, a year later, they were 68% more engaged in their maths class. Over a million people have taken that class and found it really helpful. So this is kind of where I think we are now with mindset.
A lot of teachers and others have jumped on the mindset bus or bandwagon, and they’re sharing with students. You can learn anything. But when that bus hits the wall of what I think of as fixed mathematics, those mindset messages do not hold. And what I mean by fixed mathematics is when we teach maths is a series of short questions with right and wrong answers. Students can’t see how they can grow inside those questions.
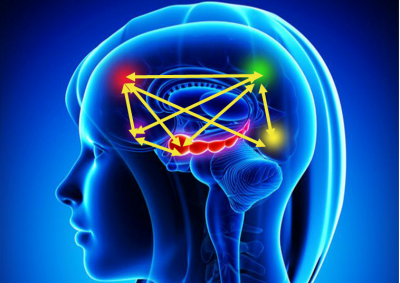And so those mindset messages of growth really fall flat for them. So one of the part of our work is sharing the importance of engaging with mathematics differently, particularly with the lens of multiplicity. I work with neuroscientists at Stanford. One of the neuroscientists I work with, called Vinod Menon, has done really important work showing that when we approach math problems, there are actually five different areas of the brain that can be activated, and we really want to activate those different parts of the brain. Also, when we approach mathematics in different ways, it causes these different pathways to fire connections.
So if we see math with numbers, but we also see it visually, it will cause a connection in the brain. Maybe we also see mathematics with words or graphs, or algorithms, or tables, or maybe we build models or we move with maths. All of these different ways of experiencing it will cause this connected brain that is so important. Recent neuroscience has even shown that they’ve looked at the brains of professional mathematicians and compared them with the brains of other academics and found that the difference is that the mathematicians are using the visual area of the brain to solve math problems. They see that activity in the visual parts of the brain.
So at Youcubed, we’re all about creating a visual mathematics experience for students, and I’d like to try it with you now. By asking you to think about a number problem just in your head, not with pen and paper, just sort of mentally think about this question. And the question I’d like you to think about is 18 times five. So maybe you can have a few moments to think about that. And the question is, how would you work this out in your head?
And I can tell you that when I ask this question of parents, when I present to parents, most of them will say that they did this in their head. They set up the traditional algorithm and then they multiplied and carried. And that is one way of working out the answer. It’s probably the hardest way of working out the answer in your head. And it’s also a problem if it’s the only way people can think about numbers.
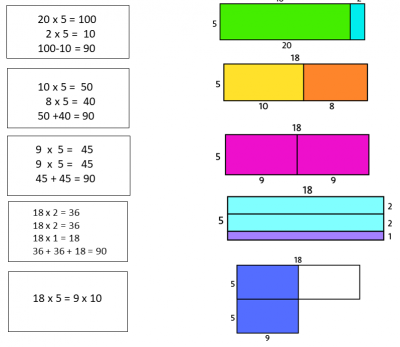And of course, there are many other ways. Some of you may have thought about 20 times five is the 100 and take off two fives. Or maybe you thought about ten times five and eight times five. Or maybe you thought about nine times fives or 18s. Or my personal favorite, perhaps you realized that 18 times five is the same as nine times ten, and that visual shows you why they are the same.
That nine times ten rectangle has the same area as an 18 times five rectangle. And right here we are getting our brains to think visually and with numbers causing those really important connections. I had an email from a teacher in Sweden just this past week, who said that their student, when they’d done an activity like this, came to them and said, so, multiplication is a kind of area. How come nobody has told me that? So, making youcubed we’re all about making numbers, visual, making mathematics tasks. Many mathematics tasks on our site are visual, but we’re also all about opening up the questions. So there’s space inside them for students to learn, space inside them for those important brain connections. You can open up any maths question. It’s not about changing the content or the curriculum.
So an example is you could ask students to work out one divided by two thirds, which is a fraction division question, and expect them to calculate the answer. That’s a totally fixed question. Or I like to remember a good friend of mine, Kathy Humphries, started her lesson by saying to students, you may know a rule for working this out. But I don’t care about the rule today. I want you to make sense of your answer and show your thinking visually.
The students then went into having rich discussions. They shared different visuals together. You can see an image there of them convincing, improving with a number line, with a pie chart. So now that same question is not a fixed question, it’s an open growth question. Sometimes we tweak questions a little bit.
So instead of asking students to work out the area of an eight by three rectangle, which has one answer, a calculation, you can ask students what rectangles can you find with an area of 24? Now they’re thinking about the relationship between length and width. They’re coming up with different visuals, hopefully. And that again completely changes that maths question from a fixed question to what I think of as a growth question. So mathematics is a conceptual and a connected subject.
Many people don’t know that. They think it’s a subject of methods and rules. And conceptual learning is a different experience in mathematics. It’s about learning more, fewer concepts, more deeply, asking questions, being curious about your learning. Reasoning is very mathematical, very important that students set out their reasons.
Maybe they can be skeptical with each other and prove to each other. That was happening in the fraction division classroom we just saw. They’re visualizing, building important mental representations. 
I teach an undergraduate class at Stanford, I’ve just finished it, and I share the different mathematicians who talk about mathematics as a conceptual connected subject. Steve Strogatz and Tydenied Bradley are both amazing mathematicians in the US, and one of my undergrads, and this happens every year, just expressed being so shocked that she had been through twelve years of learning mathematics and had never been given the idea that math was the conceptual connected subject and how important that was for her.
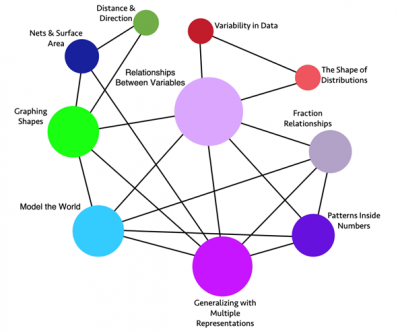And I have this experience every year with these undergrads. It’s just shocking to them that maths can be so different. So I wanted to share that in my recent work, I helped the state of California with a new mathematics framework. And as part of that, we reorganized all of the standards into what we call big ideas. So in the US, as with many other countries, teachers are given these long lists of things to teach.
And I think of mathematics as this beautiful, interconnected subject of a few ideas that are really connected to each other. But when we give standards to teachers, it’s like we chop up that interconnected web and deliver all these short statements. So we work to take all those short statements and to combine them into bigger ideas, more conceptual for every grade level, and you see grade six here, which is students of about age ten. What you see here is about eight ideas, eight to ten ideas that we say are the most important ideas. They’re bigger ideas.
They bring lots of these smaller standards together. And if we can just give students an experience of even only the ten big ideas in their grade, deeply conceptually, with rich tasks, it will serve as a foundation for everything they learn. So one of the things we’ve done is provide a set of books from grades k to eight of these deep, rich tasks. They’re really not in the published curriculum. Well, a big idea has been defined as a statement of an idea that’s central to the learning of mathematics and one that links numerous mathematical understandings into a coherent whole.
So why is conceptual learning so important? In a new book I’ve just written, I cite this study that was done where researchers said, well, teachers often share with us that they can’t teach conceptually. There’s not enough time to teach conceptually, or maybe they’ll do it, but after they’ve taught students the rules and methods. So they contrasted this. Half of the students had five lessons learning rules and methods, and then three lessons where they learned conceptually with geoboards and tiles.
They compared that with students who just got the three conceptual lessons, and it was those students who did better on every assessment they gave them.
We saw that conceptual learning in the video we watched, but what was fascinating to me is the researchers talked about how when they taught the students the methods and rules, first the students experienced what they called cognitive interference. They were so wrapped up in remembering those methods and rules, they couldn’t even think conceptually. So having the three conceptual lessons afterwards was not helpful.
So this is the approach of our summer camps that we’ve been teaching and spreading around the world. We first taught a camp at Stanford, and my goal we brought in middle school students.
My goal was to have their maths experience change from that list on the left to the list on the right. All the students came in saying they weren’t a math person. They didn’t feel good about maths. They were from different achievement levels, though. And we not only shared mindset messages with the students and the importance of struggle, we taught maths differently as a set of big conceptual ideas.
Students have many experiences to many opportunities to experience mathematics physically, mentally and physically. As you can see, the big ideas we had four that we really focused on. We had the students for four weeks, and we thought, we can teach, can really focus on those four big ideas. In four weeks. This is the results of a test that the students took before they came to us in their schools:
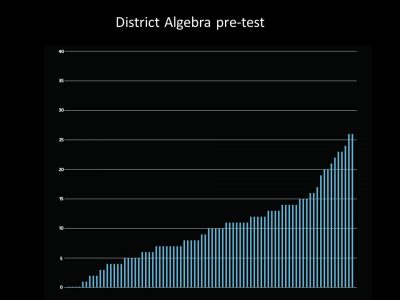
So as you can see, there was a range of achievement with some very high achievers and some students who scored zero on that test. We put them together in classes. There was no sorting by achievement. And at the end of our four week camp, we gave them that test again and we were shocked to see a huge increase for the students that was equivalent to 2.8 years of school:
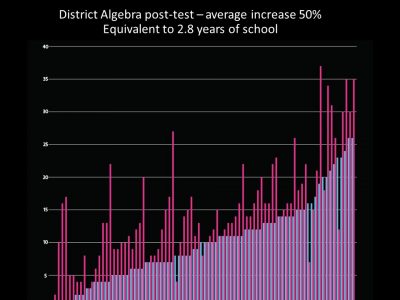
And on our website we have videos that show what happened in the camp.
But I wanted to share with you that a few years later we’ve been sharing our camp curriculum and having workshops at Stanford where we teach how to teach in these ways. And a couple of years ago we studied camps across the US and I was thrilled to see that the teachers in regular schools all around the US got the same huge boost for their students. And this graph shows you that the longer the students were in the camp, the greater the boost they received, which really tells you this is what students need, this conceptual experience even:
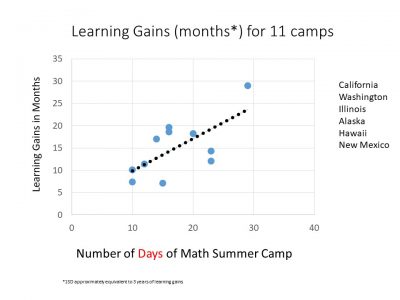
We even found in the study that when they went back to their schools, the students who attended the camps got significantly higher maths achievement in their schools. Last summer, I’m happy to share that we were asked to come to Naples in Italy and something new for us.
We were asked to train undergrads to teach our camps. Previously we’d only ever trained experienced teachers, so we thought this is going to be an interesting challenge. But it was actually fantastic. The students really got the ideas very quickly. A lot of them had had a very traumatic maths experience.
Interestingly, even though they were STEM students and successfully taught amazing camps across Italy, in Naples, in Rome last summer. So that was really fantastic to collaborate on that. And I know that the changes that happen for the students who attend these camps is to do with their getting conceptual understanding of ideas. But I also know it’s a bigger change for them that I really appreciate Etienne Wenger’s words about this. And he talks about student learning not in terms of test scores, but really in terms of a change in identity.
So this is from Wenger, he says, because learning transforms who we are and what we can do. It’s an experience of identity. It is not just an accumulation of skills and information, but a process of becoming. Even the learning that we do entirely by ourselves contributes to making us into a specific kind of person. And we accumulate skills and information not in the abstract, as ends in themselves, but in the service of an identity.
And I know that these students really change their identities as learners. During those summers in our camp and in others, I mentioned my new book, which is coming out in May, which is all about these ideas and bringing much more interesting maths to students that’s more creative and diverse with meaning. As part of the book, I talk about how we know that experts hold knowledge differently to novices. And what’s known is they hold knowledge in terms of vivid mental representation. So we worked during the summer camp to really make sure that students were developing mathematics with all these really strong mental representations.
And just to finish, I wanted to share the words of Anders Erickson, who talks about the way we build mental representations. It isn’t by thinking about something, it’s about trying to do something, failing, revising, trying again, over and over again. And he highlights, as do many experts, the importance of that time of struggle. And it was because we really wanted students to feel good about struggle that we designed a new mathematics app that I wanted to share with you that’s called struggly. I’ve designed this with a design firm in Germany who really understood the need for students to have this experience.
And you can find it at strugly.com. It’s a new endeavor. We just started it. It gives students a visual, creative experience. And unlike any other maths app, it rewards students for struggling.
It’s not about speed and answers. It’s really about that process of learning. They get badges for struggling, for brain connections, for going more deeply. So my final message is just that we need to let students dive deeply inside mathematical ideas. And it really is when they dive deeply that they discover the real beauty of mathematics.
My name is Jo Boaler. As I said, you can contact me or come to our website. And thank you for the opportunity to talk with you today.
Versione italiana