Chi ha paura della matematica?

Mettere da parte la velocità per pensare profondamente

Nella classe che abbiamo appena visto, ci sono molti aspetti che vorrei sottolineare.

Gli studenti imparano la matematica attraverso la risoluzione di problemi. Sviluppano senso del numero  usando e applicando le proprie idee. Con l’agency dello studente in primo piano, la matematica è multidimensionale. Gli studenti imparano attraverso i numeri e gruppi di numeri, le parole, i loro scambi verbali e materiali manipolativi. L’insegnante ha messo da parte la velocità e ha dato agli studenti il tempo di pensare profondamente. Come avete visto, ha sottolineato la difficoltà e l’importanza di uno sforzo impegnativo di fronte alle difficoltà. E gli studenti lavorano insieme per vedere e capire le connessioni tra concetti matematici.

L’attività sulle monete si trova sul nostro sito web, ma in realtà deriva dal “teorema” cinese “del resto”. Chiede agli studenti di cercare delle regolarità quando pensano a gruppi di numeri, e attraverso l’attività sono insegnati molti contenuti matematici.

L’importanza dei compiti difficili

Una delle cose che vorrei sottolineare oggi, su cui sto lavorando e che cerco di diffondere il più possibile, è il fatto che le difficoltà, gli sforzi che facciamo per superare le difficoltà, sono i momenti migliori per il nostro cervello. È quando nel cervello si attivano connessioni. Quindi dovremmo fare in modo che gli studenti si trovino spesso al limite delle loro possibilità. È un luogo in cui è importante trovarsi. Questo ce lo dicono le neuroscienze e ciò che conosciamo sul cervello. E ce lo dicono da tempo anche i giganti della psicologia.

Vygotsky ha parlato della zona di sviluppo prossimale, la distanza tra ciò che un allievo può fare con assistenza e ciò che può fare senza assistenza. E questo è anche il momento in cui gli studenti si impegnano all’estremo della loro comprensione. E Piaget ci ha insegnato l’importanza di trovarsi in disequilibrio.

Sviluppare una mentalità dinamica

Si è studiata molto la “mentalità volta alla crescita” o “mentalità dinamica”, in inglese “growth mindset”, e ci sono molte prove della sua importanza. Di recente, però, si assiste a una reazione contraria, per cui si dice che la “mentalità dinamica” non funziona o che i suoi effetti sono minimi. Ma questo accade quando le persone entrano negli spazi educativi, dicono agli studenti che possono imparare qualsiasi cosa e poi se ne vanno, e l’insegnamento rimane lo stesso. I dati più recenti ci dicono invece che la growth mindset ha un impatto reale. Funziona veramente quando nelle classi si sviluppa una cultura della mentalità dinamica, quando gli studenti capiscono quanto sia importante affrontare difficoltà e sfide e che il loro cervello si connette e cresce continuamente proprio attraverso lo sforzo. E funziona quando la matematica è insegnata come “disciplina dinamica” e valutata in modi che danno agli studenti opportunità di crescere e di imparare.

Sul nostro sito web, Youcubed, abbiamo una nuova sezione che presenta i dati più recenti circa l’importanza della “mentalità dinamica”. Ho sviluppato una risorsa che è stata utile a molte persone. È un corso online gratuito per gli studenti. Sei sessioni di 15 minuti che parlano della “mentalità dinamica”, e forniscono anche diverse strategie di approccio alla matematica. Ne abbiamo studiato l’impatto con uno studio controllato randomizzato in cui insegnanti di scuola media che avevano due classi di studenti, hanno seguito questo corso online con una sola classe. E abbiamo scoperto che, nonostante fosse lo stesso insegnante a insegnare alle due classi, gli studenti che avevano seguito questo breve corso online hanno ottenuto risultati significativamente più alti e, un anno dopo, erano il 68% più coinvolti nelle lezioni di matematica.

Più di un milione di persone ha seguito questo corso e lo ha trovato utile.

Molti insegnanti sono saliti – per così dire – sull'”autobus della mindset” e la presentano ai loro studenti: “puoi imparare qualunque cosa!”. Ma quando questo autobus si scontra con il muro di quella che io definisco la “matematica statica”, questi messaggi non funzionano.

Matematica statica vs matematica dinamica attraverso la lente della molteplicità

Quello che intendo per “matematica statica” è l’insegnamento della matematica come una serie di domande brevi a risposta giusta o sbagliata. Gli studenti non riescono a vedere come possono crescere “dentro” queste domande.

Per questo motivo, i messaggi sulla “mentalità dinamica” non hanno senso per loro. Quindi una parte del nostro lavoro consiste nel mostrare l’importanza di affrontare la matematica in modo diverso, in particolare attraverso la lente della molteplicità. 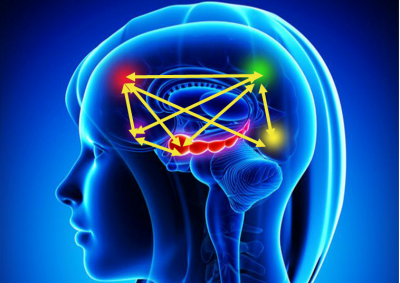Uno dei neuroscienziati di Stanford con cui lavoro, che si chiama Vinod Menon, ha svolto un lavoro molto importante, dimostrando che quando affrontiamo i problemi matematici, ci sono cinque diverse aree del cervello che possono essere attivate, e noi vogliamo proprio attivarle tutte. E quando ci avviciniamo alla matematica in modi diversi, questo fa sì che tra queste diverse parti del cervello si attivino delle connessioni.

Quindi, se vediamo la matematica con i numeri e anche in modo visivo, si creeranno connessioni nel cervello. E possiamo vedere la matematica anche con le parole, i grafici, gli algoritmi o le tabelle, oppure costruire modelli o associare la matematica al movimento del corpo. Lo sperimentare la matematica in questi diversi modi favorisce queste connessioni cerebrali così importanti. Ricerche neuroscientifiche recenti hanno persino esaminato il cervello di matematici di professione e lo hanno confrontato con quello di altri accademici, scoprendo che la differenza sta nel fatto che i matematici professionisti mostrano un’attività cerebrale più intensa nelle aree visive quando eseguono calcoli mentali.

In Youcubed siamo impegnati a creare un’esperienza visiva della matematica per gli studenti e vorrei provare a farlo con voi. Vi chiedo di pensare al problema numerico che vi pongo solo nella vostra testa, non con carta e penna, ma rispondendo a mente. Il calcolo a cui vorrei che pensaste è 18 x 5. Forse potete prendervi qualche momento per pensarci. E la domanda è: come lo risolvereste nella vostra testa, a mente?

Quando pongo questa domanda ai genitori, la maggior parte di loro risponde che nella sua testa ha impostato il calcolo in colonna, cioè ha fatto la moltiplicazione con il riporto. E questo è un modo di elaborare la risposta. Probabilmente è il modo più difficile rispondendo a mente. Ed è anche un problema se è l’unico modo in cui le persone riescono a pensare ai numeri.

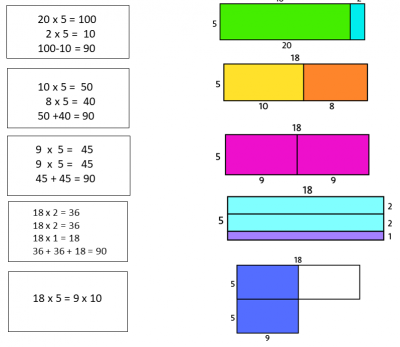Perché ci sono molti altri modi. Alcuni di voi potrebbero aver pensato che 20 volte 5 fa 100 e poi avere tolto due cinque. O forse avete pensato a 10 volte 5 e 8 volte 5. Oppure, il mio preferito, forse lo avete fatto anche voi, è che 18 x 5 è uguale a 9 x 10.

Questa immagine vi mostra perché sono uguali. Il rettangolo di dimensioni 9 x 10 ha la stessa area di un rettangolo di dimensioni 18 x 5. E qui stiamo facendo in modo che il nostro cervello pensi sia in modo visivo sia con i numeri, provocando quelle connessioni così importanti.

Proprio la settimana scorsa ho ricevuto una mail da un insegnante svedese, che mi ha raccontato che un suo studente, dopo aver svolto un’attività come questa, ha detto: “Allora, la moltiplicazione è una specie di area”. Come mai nessuno me l’ha detto prima?

Quindi, a Youcubed il nostro obiettivo è quello di trattare i numeri dal punto di vista visivo e creare attività di matematica basate sulla visualizzazione.

Domande statiche vs domande dinamiche perché “aperte”

Inoltre ci preoccupiamo di “aprire” le domande in modo che al loro interno ci sia spazio per apprendere, uno spazio per quelle importanti connessioni cerebrali. È possibile “aprire” qualsiasi domanda di matematica. Non si tratta di cambiare i contenuti o gli obiettivi curricolari.

Per esempio, si può chiedere agli studenti di risolvere il problema di 1 diviso per due terzi, che è una domanda sulla divisione con le frazioni, e aspettarsi che calcolino la risposta. Si tratta di una domanda totalmente statica. Invece una mia cara amica, Kathy Humphries, iniziava la sua lezione dicendo agli studenti: “Potreste conoscere una regola per risolvere questo problema. Ma oggi non mi interessa la regola. Voglio che spieghiate il senso della vostra risposta e che mostriate un pensiero visivo”.

Così gli studenti hanno avuto un ricco scambio, hanno proposto diverse visualizzazioni. Potete vedere una loro foto mentre lavorano insieme… Chi ha tracciato una linea dei numeri, chi un grafico a torta…  Ora la stessa domanda non è più una domanda “statica”, ma una domanda “aperta”, “dinamica”.

A volte modifichiamo un po’ le domande. Ad esempio, invece di chiedere agli studenti di calcolare l’area di un rettangolo di dimensioni 8 x 3, che è una domanda con una risposta univoca, un calcolo, si può domandare: “Quali rettangoli con area 24 si possono trovare” Ora gli studenti devono pensare alla relazione tra lunghezza e larghezza. Si spera che trovino diverse figure. E questo cambia completamente la domanda da una domanda statica, a quella che io definisco una “domanda dinamica”.

L’apprendimento concettuale in matematica

La matematica è una disciplina concettuale e interconnessa. Molte persone non lo sanno. Pensano che sia una disciplina fatta solo di metodi e regole. L’apprendimento concettuale è un’esperienza diversa in matematica. Si tratta di apprendere meno concetti, in modo più approfondito, ponendo domande, guardando con curiosità a quello che si impara. In matematica è molto importante il ragionamento, cioè il fatto che gli studenti sappiano spiegare i modi in cui procedono.

Possono mettersi in discussione l’uno con l’altro e argomentare le proprie posizioni. Questo è accaduto nell’attività sulla divisione con le frazioni che abbiamo appena visto. Gli studenti visualizzavano, costruivano rappresentazioni mentali importanti.

Tengo un corso di laurea a Stanford, l’ho appena terminato, e presento diversi matematici che parlano della matematica come disciplina concettualmente interconnessa, come Steve Strogatz e Tydenied Bradley. Una delle mie studentesse ha detto di essere rimasta colpita dal fatto che, dopo dodici anni di studio, non le era mai stato detto che la matematica fosse una disciplina concettualmente interconnessa e quanto questo fosse invece importante per lei.

Faccio questa esperienza ogni anno con i miei studenti universitari. Per loro è incredibile che la matematica possa essere così diversa da come la conoscono.

Le BIG IDEAS

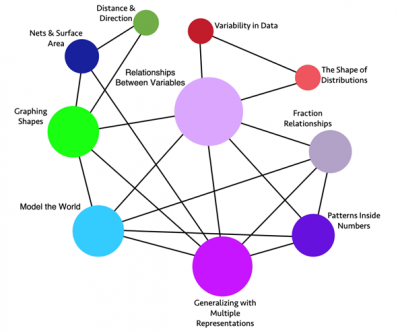Recentemente, ho aiutato lo Stato della California a elaborare un nuovo quadro di riferimento per la matematica. E come parte di questo lavoro, abbiamo riorganizzato tutti i contenuti – gli standard americani – in quelle che chiamiamo “BIG IDEAS” . Negli Stati Uniti, così come in molti altri Paesi, gli insegnanti normalmente hanno lunghi elenchi di cose da insegnare.

Al contrario, io considero la matematica come una disciplina bellissima, interconnessa, fatta di poche idee collegate tra loro. Ma quando diciamo agli insegnanti che cosa devono insegnare, spezzettiamo questa rete interconnessa in tanti brevi enunciati. Quindi, per ogni grado, per ogni anno scolare di riferimento, noi lavoriamo per combinare tutti questi brevi enunciati in idee più grandi, più concettuali. Qui vedete queste idee per il grado 6, cioè per studenti di circa dieci anni. Ci sono dieci idee, che secondo noi sono le più importanti, le cosiddette Big Ideas.

Riuniscono molti di quei contenuti più piccoli. E se riusciamo a far sperimentare agli studenti anche solo le dieci big ideas che corrispondono al loro grado, in modo profondo e concettuale, con attività ricche, questo servirà come base per tutto ciò che impareranno dopo. Per questo motivo, una delle cose che abbiamo fatto è stata quella di fornire una serie di libri dal grado 1 al grado 8 con queste attività ricche e profonde. Una BIG IDEA  è stata definita come la formulazione di un’idea centrale per l’apprendimento della matematica, che connette numerosi significati matematici in un insieme coerente.

Evidenze empiriche

Perché l’apprendimento concettuale è così importante? In un nuovo libro che ho appena scritto, cito uno studio in cui i ricercatori hanno detto: “Beh, gli insegnanti spesso ci dicono che non riescono a insegnare in modo concettuale, che non c’è abbastanza tempo per farlo, o che forse lo faranno, ma dopo aver insegnato agli studenti regole e metodi”. Quindi hanno fatto un confronto. Con metà degli studenti si sono fatte cinque lezioni per imparare regole e metodi, e poi tre lezioni in cui hanno imparato in modo concettuale con Geoboard e Algebra Tiles.

Hanno confrontato i loro risultati con quelli degli studenti che avevano ricevuto solo le tre lezioni concettuali, e hanno visto che sono proprio questi ultimi che hanno ottenuto risultati migliori in ogni valutazione.

Abbiamo osservato questo apprendimento concettuale nel video iniziale. Quello che mi ha colpito è che i ricercatori hanno detto che quando hanno insegnato per prima cosa i metodi e le regole, gli studenti hanno sperimentato quella che si chiama “interferenza cognitiva”. Erano così presi dal ricordare metodi e regole che non riuscivano a pensare in modo concettuale. Quindi le tre lezioni concettuali successive non sono state utili. Questo è l’approccio dei nostri campi estivi.

L’approccio dei campi estivi

La prima volta abbiamo tenuto un campo a Stanford rivolto agli studenti delle scuole medie.

Il mio obiettivo era far sì che cambiasse la loro esperienza della matematica, passando dall’elenco a sinistra a quello a destra. Tutti gli studenti sono arrivati dicendo che non avevano una mente matematica. Non si sentivano portati per la matematica. Anche se avevano livelli molto diversi di risultati. Non solo abbiamo parlato agli studenti della mentalità dinamica e dell’importanza di impegnarsi, ma abbiamo insegnato la matematica in modo diverso, come un insieme di grandi idee concettuali.

Gli studenti hanno avuto molte opportunità di sperimentare la matematica, a mente e con il loro corpo. Come potete vedere, le big ideas su cui ci siamo concentrati sono quattro. Siamo stati con gli studenti per quattro settimane e abbiamo pensato che potevamo concentrarci su queste quattro grandi idee.

Questi sono i risultati di un test che gli studenti hanno fatto prima di venire da noi, nelle loro scuole:

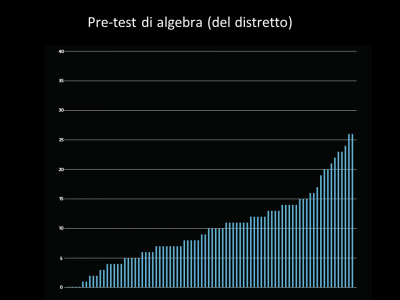
Come potete notare, la gamma dei risultati era molto ampia. Alcuni studenti avevano ottenuto risultati molto alti e altri un punteggio pari a zero. Nelle nostre classi li abbiamo messi insieme. Non c’è stata una suddivisione sulla base dei risultati. Alla fine del campo, dopo quattro settimane, abbiamo riproposto loro il test e siamo rimasti sorpresi dell’enorme miglioramento, equivalente a 2,8 anni di scuola:

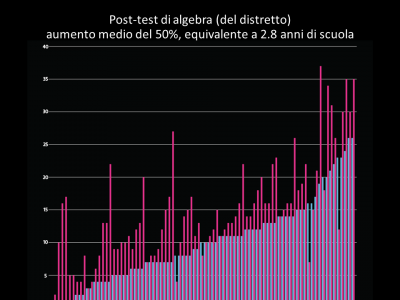
Sul nostro sito web abbiamo dei video che mostrano che cosa è successo durante il campo.

Un’altra cosa che volevo raccontarvi è che da qualche anno presentiamo il programma del campo e teniamo seminari a Stanford in cui formiamo a insegnare in questo modo. Un paio di anni fa abbiamo studiato i risultati di questi campi e sono stata molto contenta quando ho visto che insegnanti di scuole pubbliche in diverse parti degli Stati Uniti hanno ottenuto lo stesso enorme miglioramento per i loro studenti.

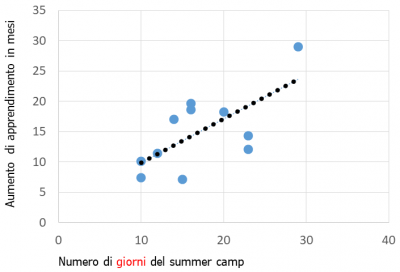
Il grafico sopra mostra che più a lungo gli studenti sono stati nel campo, maggiore è stato l’aumento dei loro risultati, e questo significa che quello di cui gli studenti hanno bisogno è proprio questa esperienza concettuale. Nello studio abbiamo anche rilevato che, anche tornati a scuola, gli studenti che hanno frequentato i campi hanno ottenuto in matematica risultati significativamente più alti.

L’estate scorsa, ci è stato chiesto di venire a Napoli, in Italia. Ci è stato chiesto di formare dei laureandi come insegnanti dei nostri campi. In precedenza avevamo formato solo insegnanti esperti, quindi abbiamo pensato che questa sarebbe stata una sfida interessante. Ed è stato entusiasmante. Gli studenti hanno recepito le idee molto rapidamente. Molti di loro avevano avuto un’esperienza traumatica con la matematica, pur essendo studenti di discipline STEM.

Quando hanno tenuto loro stessi dei campi in Italia, a Napoli e a Roma, è andata molto bene.

Cambiamento d’identità

So che il cambiamento che avviene per gli studenti che partecipano a questi campi ha a che fare con una comprensione concettuale delle idee. Ma so anche che si tratta di un cambiamento ancora più grande del solo miglioramento dei risultati in matematica. A questo proposito, mi piace quello che dice Etienne Wenger quando parla dell’apprendimento degli studenti non in termini di punteggi dei test, ma in termini di cambiamento di identità.

Dice: “Poiché l’apprendimento trasforma ciò che siamo e ciò che possiamo fare, è un’esperienza di identità. Non si tratta solo di un accumularsi di competenze e informazioni, ma di un processo che ha a che fare con chi diventiamo. Anche l’apprendimento che facciamo interamente da soli contribuisce a farci diventare quella particolare persona che siamo. E accumuliamo competenze e informazioni non in astratto, fini a se stesse, ma al servizio di un’identità.”

So che per i ragazzi, durante queste estati nei nostri campi, cambia davvero la loro identità di studenti.

Ho parlato di questo nel mio nuovo libro, che uscirà a maggio, incentrato su queste idee e sulla possibilità di fare incontrare agli studenti una matematica più interessante, più creativa e ricca di significati. Nel libro dico che sappiamo che gli esperti posseggono la conoscenza in modo diverso dai novizi. La posseggono come rappresentazione mentale vivida. Quindi, abbiamo lavorato durante il campo estivo per assicurarci che gli studenti sviluppassero la matematica attraverso queste forti rappresentazioni mentali.

“Struggling”, impegnarsi nella difficoltà

E per concludere, vorrei condividere le parole di Anders Erickson, che parla del modo in cui costruiamo le rappresentazioni mentali. Non si tratta di pensare a qualcosa, ma di provare a fare qualcosa, di fallire, di correggere, di riprovare, ancora e ancora. E sottolinea, come molti altri esperti, l’importanza di questo tempo in cui ci si scontra con la difficoltà, con l’impegno, in inglese “struggle”.

.

.

Proprio perché volevamo che gli studenti si sentissero a proprio agio con questa “lotta”, abbiamo progettato una nuova applicazione per la matematica, chiamata struggly. L’ho progettata in collaborazione con un’azienda di design tedesca che ha capito l’importanza di far vivere agli studenti esperienze di questo tipo.

Potete trovarla su struggly.com. È una nuova impresa. Offre agli studenti un’esperienza visiva e creativa della matematica. E a differenza di qualsiasi altra app per la matematica, premia gli studenti quando si impegnano.

Non è questione di velocità e di risposte. È questione di quel processo di apprendimento. Gli studenti ricevono badge per la loro perseveranza nello sforzo, le connessioni mentali, per essere andati più in profondità. Quindi il mio messaggio finale è che dobbiamo permettere agli studenti di immergersi profondamente nelle idee matematiche. Ed è proprio quando si immergono in profondità che scoprono la vera bellezza della matematica.

Grazie per l’opportunità di parlare con voi oggi.